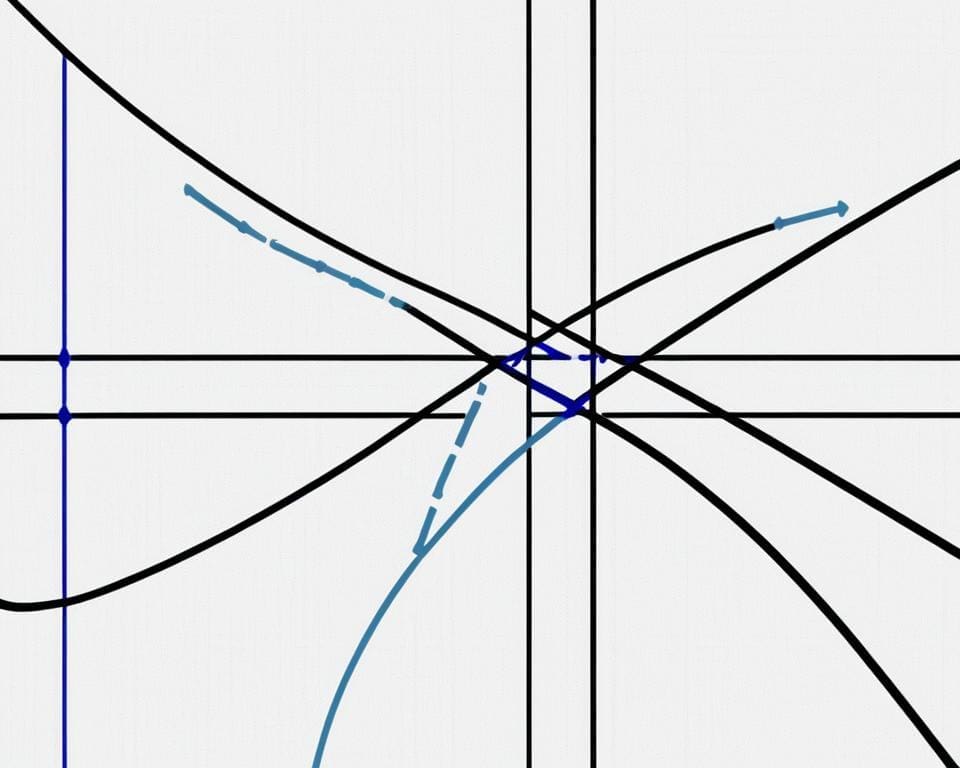
Een loodrechte lijn is een belangrijk concept in de meetkunde. Het verwijst naar een lijn die een hoek van 90 graden maakt met een andere lijn of oppervlak. Een loodrechte lijn staat loodrecht op een ander object, waardoor het een speciale relatie heeft met de objecten waarmee het in contact komt.
Om een beter begrip te krijgen van wat een loodrechte lijn is, is het belangrijk om de definitie ervan te begrijpen. Een loodrechte lijn kan worden gedefinieerd als een lijn die een andere lijn snijdt en een hoek van 90 graden vormt. Deze lijn wordt ook wel een “loodlijn” genoemd, omdat deze loodrecht op de andere lijn staat.
Een loodrechte lijn heeft verschillende eigenschappen die het uniek maken. Ten eerste is de hoek tussen twee loodrechte lijnen altijd 90 graden. Dit betekent dat de lijnen elkaar kruisen en elkaar snijden op een punt waar beide hoeken 90 graden zijn.
Daarnaast kunnen loodrechte lijnen worden geïdentificeerd aan de hand van hun richtingscoëfficiënten. Als twee lijnen loodrecht op elkaar staan, is het product van hun richtingscoëfficiënten gelijk aan -1. Dit concept van loodrechte lijnen is essentieel in de wiskunde en wordt vaak toegepast in verschillende toepassingen.
In de volgende secties gaan we dieper in op hoe je een loodrechte lijn kunt herkennen, wat de formule is om een loodrechte lijn te berekenen en hoe loodrechte lijnen worden toegepast in verschillende contexten. We bespreken ook de eigenschappen van loodrechte lijnen en het belang ervan in de praktijk en de meetkunde.
Hoe herken je een loodrechte lijn?
Om een loodrechte lijn te herkennen, is het belangrijk om de eigenschappen van een loodrechte lijn te begrijpen en te weten hoe je kunt bepalen of een lijn loodrecht is op een andere lijn. Er zijn verschillende methoden en technieken die je kunt gebruiken om dit te doen.
Een van de eigenschappen van een loodrechte lijn is dat de hoeken die het vormt met andere lijnen 90 graden zijn. Dit betekent dat als je twee lijnen hebt en de hoek tussen hen 90 graden is, deze lijnen loodrecht op elkaar staan.
Je kunt ook de richtingscoëfficiënten van de lijnen vergelijken om te bepalen of ze loodrecht zijn. Als de richtingscoëfficiënt van de ene lijn het negatieve omgekeerde is van de richtingscoëfficiënt van de andere lijn, dan zijn de lijnen loodrecht op elkaar.
Daarnaast kun je ook gebruik maken van het meetkundige concept van de lengte van de zijden. Als je een rechthoekige driehoek hebt waarvan de zijden voldoen aan de stelling van Pythagoras, dan kun je concluderen dat de lijnen loodrecht zijn.
De eigenschappen van een loodrechte lijn zijn essentieel bij het oplossen van meetkundige vraagstukken en het begrijpen van de relatie tussen verschillende lijnen. Door deze eigenschappen te herkennen en te begrijpen, kun je nauwkeurige metingen en berekeningen uitvoeren.
Met de kennis van deze eigenschappen kun je een lijn snel en eenvoudig herkennen als loodrecht op een andere lijn. Dit is vooral handig bij het oplossen van meetkundige problemen en het construeren van nauwkeurige figuren.
De formule voor een loodrechte lijn
Een loodrechte lijn is een lijn die een hoek van 90 graden maakt ten opzichte van een andere lijn. Maar hoe kun je bepalen of twee lijnen loodrecht op elkaar staan? Hiervoor is er een formule die je kunt gebruiken.
Om de formule voor een loodrechte lijn te begrijpen, moeten we kijken naar de richtingscoëfficiënten van de twee lijnen. De richtingscoëfficiënt is een getal dat aangeeft hoe steil de lijn is. Het is als het ware de helling van de lijn.
De formule luidt als volgt:
Als twee lijnen loodrecht op elkaar staan, dan is het product van hun richtingscoëfficiënten -1.
Met deze formule kun je de loodrechte lijn berekenen door de richtingscoëfficiënten van beide lijnen te vergelijken. Als het product van de richtingscoëfficiënten -1 is, dan staan de lijnen loodrecht op elkaar.
Een voorbeeld ter verduidelijking: stel dat de richtingscoëfficiënt van de ene lijn 2 is en de richtingscoëfficiënt van de andere lijn -0.5. Als we deze getallen met elkaar vermenigvuldigen, krijgen we -1. Dit betekent dat de lijnen loodrecht op elkaar staan.
De formule voor een loodrechte lijn is dus een handige tool om te bepalen of twee lijnen loodrecht op elkaar staan. Door de richtingscoëfficiënten te vergelijken en het product te berekenen, kun je snel en eenvoudig de relatie tussen de lijnen bepalen.
Door gebruik te maken van de formule voor een loodrechte lijn, kun je gemakkelijk de hoek tussen twee lijnen bepalen en diverse meetkundige problemen oplossen. Het begrijpen en toepassen van deze formule is essentieel voor een goed begrip van loodrechte lijnen en hun eigenschappen.
Toepassingen van loodrechte lijnen
In dit gedeelte zullen we verschillende praktische toepassingen van loodrechte lijnen verkennen. Loodrechte lijnen zijn niet alleen een abstract concept uit de meetkunde, maar hebben ook talloze toepassingen in het dagelijks leven en verschillende vakgebieden.
Een van de belangrijkste toepassingen van loodrechte lijnen is in de architectuur. Bij het ontwerpen van gebouwen moeten architecten ervoor zorgen dat muren, balken en kolommen loodrecht op elkaar staan om de structuur van het gebouw te garanderen. Het gebruik van loodrechte lijnen zorgt voor stabiliteit en duurzaamheid, waardoor een gebouw veilig en stevig blijft.
In de bouwsector worden loodrechte lijnen ook gebruikt bij het leggen van vloeren, tegels en andere structurele elementen. Het gebruik van een loodlijn helpt vakmensen om ervoor te zorgen dat alles perfect recht en loodrecht is, waardoor een professioneel resultaat wordt bereikt.
Daarnaast spelen loodrechte lijnen een belangrijke rol in de meetkunde. Meetkundige berekeningen en constructies maken gebruik van loodrechte lijnen om hoeken te meten en te creëren. Bij het tekenen van meetkundige figuren, zoals vierkanten, rechthoeken en driehoeken, zijn loodrechte lijnen van essentieel belang.
“Loodrechte lijnen zijn onmisbaar bij het ontwerpen van gebouwen, het leggen van vloeren en het construeren van meetkundige figuren.”
Buiten de bouw en de meetkunde worden loodrechte lijnen ook gebruikt in andere vakgebieden. In de wiskunde worden bijvoorbeeld loodrechte lijnen gebruikt in de trigonometrie en het berekenen van afstanden en hoeken. In de natuurkunde spelen loodrechte lijnen een rol bij het analyseren van krachten en het begrijpen van de werking van hefbomen en palen.
Kortom, loodrechte lijnen hebben vele praktische toepassingen in de architectuur, de bouw, de meetkunde en andere vakgebieden. Ze zorgen voor stabiliteit, precisie en structuur in verschillende constructies en berekeningen.

Loodrechte lijnen in de meetkunde
In de meetkunde spelen loodrechte lijnen een belangrijke rol. Ze helpen ons bij het begrijpen van de geometrische vormen en figuren om ons heen. Een loodrechte lijn is een lijn die onder een hoek van 90 graden staat ten opzichte van een andere lijn. Deze lijnen hebben unieke eigenschappen die ze onderscheiden van andere lijnen in de meetkunde.
De constructie van loodrechte lijnen kan worden bereikt door verschillende methoden van meetkunde. Een veelgebruikte methode is de constructie met behulp van een passer en een liniaal. Door zorgvuldig gebruik te maken van deze meetinstrumenten kunnen we een loodrechte lijn constructie uitvoeren en de exacte hoek van 90 graden verkrijgen.
De loodrechte lijn constructie is van cruciaal belang bij het tekenen en ontwerpen van meetkundige figuren. Het maakt het mogelijk om nauwkeurige metingen en berekeningen uit te voeren, waardoor we complexe vormen kunnen analyseren en begrijpen. Daarnaast is de constructie van loodrechte lijnen essentieel in architectuur, bouwkunde, landmeting en tal van andere disciplines waarin geometrische principes worden toegepast.
De loodrechte lijnen in de meetkunde bieden ons een dieper inzicht in de structuur en eigenschappen van geometrische vormen. Ze helpen ons bij het begrijpen van de relaties tussen verschillende lijnen en het oplossen van meetkundige problemen. Door de constructie van loodrechte lijnen kunnen we de nauwkeurigheid en precisie bereiken die nodig zijn voor de analyse en toepassing van meetkundige concepten.
Eigenschappen van loodrechte lijnen
In dit gedeelte zullen we de belangrijkste eigenschappen van loodrechte lijnen behandelen. Het begrijpen van deze eigenschappen is essentieel om het concept van loodrechte lijnen volledig te kunnen waarderen en toepassen. Een loodrechte lijn is een lijn die een hoek van 90 graden vormt met een andere lijn of vlak. Deze eigenschap maakt loodrechte lijnen uniek en nuttig in verschillende situaties en disciplines, zoals meetkunde, bouwkunde en architectuur.
Hoeken gevormd door loodrechte lijnen
De eigenschap waar loodrechte lijnen om bekend staan, is de vorming van een rechte hoek. Een rechte hoek is een hoek van 90 graden, wat betekent dat de loodrechte lijnen elkaar precies snijden om deze hoek te vormen. Deze hoek is recht, wat betekent dat hij geen afwijking heeft en perfect loodrecht is. Dit biedt nauwkeurigheid en stabiliteit in verschillende wiskundige en praktische toepassingen.
Een voorbeeld van loodrechte lijnen in de praktijk is het ontwerp van vierkante en rechthoekige vormen. De zijden van deze vormen zijn loodrecht op elkaar, waardoor ze perfecte rechte hoeken vormen. Dit maakt ze ideaal voor het bouwen van stevige structuren en het creëren van symmetrische en evenwichtige ontwerpen.
De eigenschappen van loodrechte lijnen, zoals het vormen van rechte hoeken, zijn van fundamenteel belang in de meetkunde. Ze helpen bij het oplossen van complexe vraagstukken en het begrijpen van de relaties tussen verschillende lijnen en vlakken.
Eigenschappen toepasbaar in verschillende situaties
Naast het vormen van rechte hoeken, hebben loodrechte lijnen andere eigenschappen die nuttig zijn in verschillende situaties. De loodrechte lijnconstructie wordt vaak gebruikt voor het bepalen van afstanden, het markeren van rechte hoeken en het construeren van parallelle lijnen. Deze eigenschappen zijn belangrijk in vakgebieden zoals engineering, architectuur en landmeetkunde.
De eigenschappen van loodrechte lijnen zijn ook van toepassing op andere concepten in de wiskunde, zoals de stelling van Pythagoras. Deze stelling stelt dat in een rechthoekige driehoek het kwadraat van de lengte van de hypotenusa gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden. Loodrechte lijnen en rechte hoeken spelen een fundamentele rol in het begrijpen en toepassen van deze stelling.
Kortom, loodrechte lijnen hebben unieke eigenschappen die ze onderscheiden van andere lijnen. Hun vermogen om perfecte rechte hoeken te vormen en toepasbaarheid in verschillende disciplines maken ze waardevol in de wiskunde en in praktische toepassingen.
Loodrechte lijn in de praktijk
Waarom zijn loodrechte lijnen belangrijk? In het dagelijks leven en in verschillende beroepen spelen loodrechte lijnen een cruciale rol. Ze voorzien ons van een belangrijk referentiepunt en helpen ons bij het oplossen van problemen en het maken van nauwkeurige metingen.
Als voorbeeld kunnen we kijken naar de architectuur. Bij het ontwerpen van gebouwen en constructies is het essentieel om loodrechte lijnen te gebruiken om de juiste afmetingen en verhoudingen te waarborgen. Loodrechte lijnen zorgen ervoor dat de muren, ramen en deuren perfect in harmonie zijn en dragen bij aan de stabiliteit en stevigheid van het gebouw.
Een ander praktisch voorbeeld is te vinden in de bouwsector. Bij het leggen van vloeren, tegels of parket is het van groot belang om loodrechte lijnen te gebruiken als leidraad. Dit garandeert een nauwkeurige en gelijkmatige plaatsing, waardoor een professionele afwerking wordt bereikt.
Daarnaast zijn loodrechte lijnen van onschatbare waarde in de meetkunde. Ze stellen ons in staat om hoeken, lengtes en afstanden te meten, en om symmetrie en evenwicht in ontwerpen en constructies te creëren. Denk aan de toepassing van loodrechte lijnen bij het tekenen van haakse driehoeken of bij het construeren van parallellogrammen.
De precisie en functionaliteit die loodrechte lijnen bieden, maken ze onmisbaar in verschillende beroepen en alledaagse situaties.
Of je nu een architect, bouwvakker, wiskundige of gewoon een huiseigenaar bent, het begrijpen en kunnen werken met loodrechte lijnen is van vitaal belang. Het stelt ons in staat om nauwkeurige metingen uit te voeren, professionele resultaten te behalen en gestructureerde ontwerpen te creëren.
Als je meer wilt weten over het belang van loodrechte lijnen en hoe je ze in de praktijk kunt gebruiken, lees dan verder naar het volgende gedeelte.
Belang van loodrechte lijnen
In de wereld van meetkunde en andere disciplines speelt de loodrechte lijn een uiterst belangrijke rol. Het begrijpen van de betekenis en het concept van een loodrechte lijn is essentieel voor verschillende toepassingen en berekeningen. Zowel op wiskundig als praktisch niveau heeft de loodrechte lijn grote waarde.
Een loodrechte lijn is een lijn die een hoek van 90 graden vormt met een andere lijn, de zogenaamde basislijn. Deze eigenschap biedt ons veel nuttige mogelijkheden in verschillende situaties. Bijvoorbeeld, in de architectuur en constructie wordt de loodrechte lijn gebruikt om muren, kolommen en andere structuren loodrecht op elkaar te laten staan, waardoor stabiliteit wordt gegarandeerd.
De betekenis van een loodrechte lijn gaat echter verder dan alleen de constructie en het ontwerp van gebouwen. In de meetkunde is deze eigenschap van cruciaal belang bij het bepalen van afstanden, hoeken en het oplossen van meetkundige problemen. Het stelt ons ook in staat om nauwkeurige metingen en berekeningen uit te voeren, wat essentieel is in wetenschappelijke en technische disciplines.
“De loodrechte lijn vormt de basis voor vele meetkundige concepten en is daarmee een fundamenteel element in de wereld van de geometrie.”
Praktische toepassingen van loodrechte lijnen
De loodrechte lijn heeft een breed scala aan praktische toepassingen buiten de geometrie en de constructie-industrie. In navigatie wordt bijvoorbeeld gebruik gemaakt van loodrechte lijnen om de koers van een schip te bepalen ten opzichte van Noord of de horizon. In het dagelijks leven helpt het begrijpen van loodrechte lijnen ons bij het parkeren van auto’s, het plaatsen van meubels en het uitlijnen van voorwerpen.
Kortom, het belang van loodrechte lijnen kan niet worden onderschat. Het is een concept dat ons helpt onze omgeving te begrijpen, nauwkeurige metingen uit te voeren en stabiele constructies te creëren. Door de betekenis en toepassingen van loodrechte lijnen te begrijpen, kunnen we een solide basis leggen voor verdere studie en toepassing in verschillende disciplines.
Hoe gebruik je loodrechte lijnen?
Als je eenmaal begrijpt wat een loodrechte lijn is en hoe je deze kunt herkennen, is het tijd om te leren hoe je ze kunt gebruiken in verschillende situaties. Hier zijn enkele praktische tips en technieken om loodrechte lijnen te tekenen, meten en toepassen:
- Gebruik een geodriehoek of een T-vierkant om nauwkeurig loodrechte lijnen te tekenen. Plaats de basislijn en teken vervolgens een lijn vanuit het punt waar je de loodrechte lijn wilt hebben, die de basislijn snijdt met een rechte hoek.
- Wanneer je een gebouw of structuur construeert, is het belangrijk om loodrechte lijnen te gebruiken om ervoor te zorgen dat de muren, deuren en ramen perfect verticaal en horizontaal zijn.
- In de wiskunde kunnen loodrechte lijnen worden gebruikt om hoeken te creëren. Bijvoorbeeld, als je een rechthoek wilt tekenen, moet je er zeker van zijn dat de zijden loodrecht op elkaar staan.
- In de meetkunde kunnen loodrechte lijnen worden gebruikt om hoogtes, dieptes en afstanden te meten. Een waterpas is een handig hulpmiddel om ervoor te zorgen dat iets perfect horizontaal of verticaal is.
- In de architectuur worden loodrechte lijnen gebruikt om de stabiliteit en evenwicht van een structuur te waarborgen. Ze helpen bij het berekenen van de belasting op een gebouw en bepalen de positie van pilaren en steunmuren.
Het gebruik van loodrechte lijnen is essentieel in veel vakgebieden, waaronder de bouw, architectuur, meetkunde en engineering. Door te weten hoe je loodrechte lijnen kunt herkennen en gebruiken, kun je nauwkeurige metingen en constructies maken, en problemen oplossen op een effectieve en efficiënte manier.
“Loodrechte lijnen zijn de ruggengraat van de geometrie. Ze bieden structuur, evenwicht en stabiliteit in onze fysieke wereld.” – Paulo de Geometrist
Eigenschappen van loodrechte lijnen samengevat
In dit laatste gedeelte willen we graag de belangrijkste eigenschappen en concepten met betrekking tot loodrechte lijnen samenvatten. Het begrijpen van deze eigenschappen is essentieel voor het werken met loodrechte lijnen in verschillende contexten.
Ten eerste is een loodrechte lijn een lijn die een hoek van 90 graden vormt met een andere lijn. Dit betekent dat de helling van de ene lijn de negatieve omgekeerde waarde is van de helling van de andere lijn. Dit is een belangrijke eigenschap om te herkennen of twee lijnen loodrecht op elkaar staan.
Een andere belangrijke eigenschap van loodrechte lijnen is dat ze elkaar snijden op één enkel punt. Dit snijpunt wordt het “snijpunt” van de lijnen genoemd en is een cruciaal concept bij het oplossen van problemen waarbij loodrechte lijnen betrokken zijn.
Door de eigenschappen van loodrechte lijnen te begrijpen, kunnen we ze gebruiken in verschillende situaties. Ze worden veel gebruikt in de architectuur en de bouw om precieze metingen en constructies uit te voeren. Daarnaast zijn ze ook van toepassing in de meetkunde en hebben ze praktische toepassingen in ons dagelijks leven.
FAQ
Wat is een loodrechte lijn?
Een loodrechte lijn is een lijn die een hoek van 90 graden vormt met een andere lijn of een vlak. Het is de kortste afstand tussen twee punten en staat loodrecht op het vlak waarop het ligt.
Hoe herken je een loodrechte lijn?
Een loodrechte lijn kan worden herkend aan de eigenschap dat de richtingscoëfficiënt van de ene lijn het negatieve omgekeerde is van de richtingscoëfficiënt van de andere lijn.
Wat is de formule voor een loodrechte lijn?
De formule voor een loodrechte lijn wordt bepaald door de richtingscoëfficiënt van de ene lijn te vermenigvuldigen met het negatieve omgekeerde van de richtingscoëfficiënt van de andere lijn.
Wat zijn toepassingen van loodrechte lijnen?
Loodrechte lijnen worden veel gebruikt in de architectuur en constructie, bij het leggen van vloeren, muren en plafonds. Ze spelen ook een belangrijke rol in de meetkunde en kunnen worden toegepast bij het oplossen van wiskundige vraagstukken.
Hoe worden loodrechte lijnen gebruikt in de meetkunde?
Loodrechte lijnen worden veelvuldig gebruikt bij het construeren van meetkundige figuren, zoals vierkanten, rechthoeken en driehoeken. Ze helpen bij het bepalen van hoeken en het creëren van symmetrie in de vormen.
Wat zijn de belangrijkste eigenschappen van loodrechte lijnen?
Loodrechte lijnen vormen een hoek van 90 graden met elkaar, hun richtingscoëfficiënten zijn het negatieve omgekeerde van elkaar en de lengte van een loodrechte lijn is de kortste afstand tussen twee punten.
Waarom zijn loodrechte lijnen belangrijk?
Loodrechte lijnen zijn belangrijk omdat ze nauwkeurige metingen en constructies mogelijk maken. Ze dragen bij aan de stabiliteit van bouwwerken en zijn van essentieel belang bij het oplossen van wiskundige vraagstukken en meetkundige problemen.
Wat is de betekenis van een loodrechte lijn?
De betekenis van een loodrechte lijn ligt in het concept van 90 graden hoeken en de nauwkeurigheid die ze bieden in verschillende disciplines. Ze vertegenwoordigen de kortste afstand tussen twee punten en hebben praktische toepassingen in de bouw, architectuur en wiskunde.
Hoe gebruik je loodrechte lijnen?
Loodrechte lijnen kunnen worden gebruikt bij het tekenen van nauwkeurige constructies, bij het bepalen van hoeken en bij het maken van metingen. Ze kunnen ook worden toegepast bij het oplossen van vraagstukken waarbij symmetrie en rechte hoeken nodig zijn.
Wat zijn de belangrijkste eigenschappen van loodrechte lijnen?
De belangrijkste eigenschappen van loodrechte lijnen zijn dat ze een hoek van 90 graden vormen, dat hun richtingscoëfficiënten elkaars negatieve omgekeerden zijn en dat ze de kortste afstand tussen twee punten vertegenwoordigen.
Hoe kan ik loodrechte lijnen samenvatten?
Loodrechte lijnen vormen een essentieel concept in de meetkunde en andere disciplines. Ze worden gekenmerkt door hun hoek van 90 graden en de nauwkeurigheid en stabiliteit die ze bieden. Ze zijn belangrijk bij het bouwen en meten, en helpen bij het oplossen van verschillende vraagstukken en problemen.